高中生 自慰

在咱们的过去生活中，经常会遇到种种不雅点的对立，进而激勉强烈的争论，也经常际遇扭曲，不得不苦思冥想为我方谈论。

然则，最理想的情况是，争论的两边都能在莫得迷漫强有劲的左证时保持严慎，不仅不在言辞上逞强，内心也相通不下判断，恭候更充分的左证出现。

这在面临扭曲时尤为勤恳，因为一个东谈主要自证皑皑往往丧祭常困难的。

然则，履行中很少有东谈主能达到这种感性想维的水平。

争论的依据往往滑向无餍论的地方，比如对于选举作弊、登月作秀、罗斯柴尔德眷属或共济会限度全球经济和政zhi等。

难以自证皑皑的扭曲更是如斯。

是以，今天咱们来仔细谈谈对于无餍论方面的常识。

01 无餍论的产生：拉姆皆定理的视角

弗兰克·普伦普顿·拉姆皆

拉姆皆是谁？

弗兰克·普伦普顿·拉姆皆（Frank Plumpton Ramsey）于1903年2月22日配置在英国剑桥。

他的父亲阿瑟·拉姆皆（Arthur Ramsey）是一位驰名的数学家，母亲玛丽·拉姆皆（Mary Ramsey）则是一位超越的作者。

拉姆皆从小就推崇出不凡的才智和学习能力，年仅19岁便投入剑桥大学三一学院，运转了他的学术糊口。

尽管拉姆皆的一世仅有短短的26年，但他在数学、形而上学和经济学畛域的孝顺却是弘大的。在数学畛域，他提议的拉姆皆定理（Ramsey's Theorem）成为组合数学和图论的勤恳基石。

那么，无餍论为何会存在？

其实，这个就不错用上头所提到的拉姆皆定理（Ramsey's Theory）来解释。

这个定理的笔墨描写是这么的：

对放纵整数 a 和 b，若参加约聚的东谈主数 n 迷漫大，则无论他们之间相识与不相识的关系如何，都必定会有 a 个东谈主相识，能够 b 个东谈主互不相识。当给定 a 和 b 时，保证前边陈述的最小值就叫作拉姆皆数 R (a，b)，其值取决于 a 和 b。

这个严谨的数学表述听起来似乎有些复杂，但咱们不错将其形象化。

比如，在举办一个约聚时，咱们庸碌有两个初志：

一是但愿练习的东谈主在一皆玩得更欣喜，

二是但愿生分东谈主之间建筑新的辩论。

若是但愿约聚上至少有 3 个东谈主之前就相互意志，能够至少有 3 个东谈主互不料志，那么最少需要邀请几许东谈主呢？

这个数字的拉姆皆数 R 等于 6，而 a 和 b 诀别是 3 和 3。

相通的，若是条目至少 4 个东谈主相互意志，能够 4 个东谈主互不料志，那拉姆皆数 R 等于 18；

若是条目至少 3 个东谈主相互意志，况兼 9 个东谈主互不料志，拉姆皆数等于 36。

这个求解进程是很复杂的高中生 自慰，触及到图论的许多常识，如下图，环球了解即可！

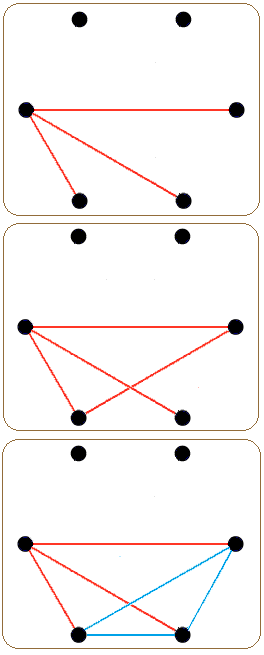
拉姆皆定理诠释图示：R(3，3)=6

可能有东谈主会感到困惑：咱们不是在策动无餍论的产生吗？为什么会扯到数学游戏？

其实，若是咱们反过来厚实刚才的求解进程，就能更好地厚实无餍论的酿成。

设计咱们举办一个约聚，莫得特定的决议，乱伦qvod既链接顶安排熟东谈主之间的互动，也不有意促进生分东谈主之间的辩论。

比如，在一场游戏的对决中，自觉聚会了许多不雅众，只消不雅世东谈主数达到6个，就有可能出现3个东谈主相互不料志能够3个东谈主之前就相互意志的情况。

相通地，只消东谈主数达到36个，不仅有3个东谈主之前相互意志或不料志的比例大大加多，以致9个东谈主之前互不相识的可能性也从数学上来说不再是零。

因此，东谈主数是一个基本盘。只消数值够大，这些东谈主中就会出现多半的谙习关系。

为了更好地厚实无餍论的产生，咱们不错用字母代替东谈主。

铭记在咱们中学英语课上频频玩一个寓教于乐的游戏，等于从一个大表格中找出英语单词。

假定有一个20×20的表格，每个格子里有一个字母，然后憨厚给咱们5分钟时辰，让咱们从中找出种种暗示颜料的单词，谁在5分钟内找出的单词最多，谁就不错除名今晚的一部分英语功课。

环球会横着找、竖着找、斜着找。

有些词，比如“red”因为很短，是以很容易找到；

“yellow”也很好找，因为以“y”开首的颜料词很少。

有期间，憨厚也会让咱们找暗示数字的英文单词。

这种表格是怎样制作的呢？

憨厚其实是先把一些暗示颜料或数字的单词填进去，比如说填6个，然后再就地填入其他字母，完成这个谜题。这种样式是从上至下缱绻的谜题，学生最多只可找出6个单词。

但还有一种更通俗的出题样式，等于裁汰条目，只需找出任何单词，不限度单词的类别。

这么的话，不错把表格弄大一些，比如30×30，然后在每个格子里就地填入字母。

这么一个包含900个字母的大表格里，深信会出现许多出东谈主预见的单词。

“许多出东谈主预见的单词”，是什么真谛呢？

咱们知谈，字母与字母之间有不同的关联度，比如字母“S”背面随着“H”的概率要大于随着其他字母的概率。

在这种情况下，这些关联度不同的字母会在就地摆列后构成单词。

而这些单词并不是缱绻出来的，以致就地填字母的东谈主也无法预感会出现这些正好的单词。

当东谈主们能干到这些字母能构成单词，能够这些单词正好和他们最近的担忧相干时，就可能会觉得，30×30的表格在冥冥中向他们传递着某种信号。

咱们不错通过法子(www.bit.ly/findaword）来生成一个就地字母表格。

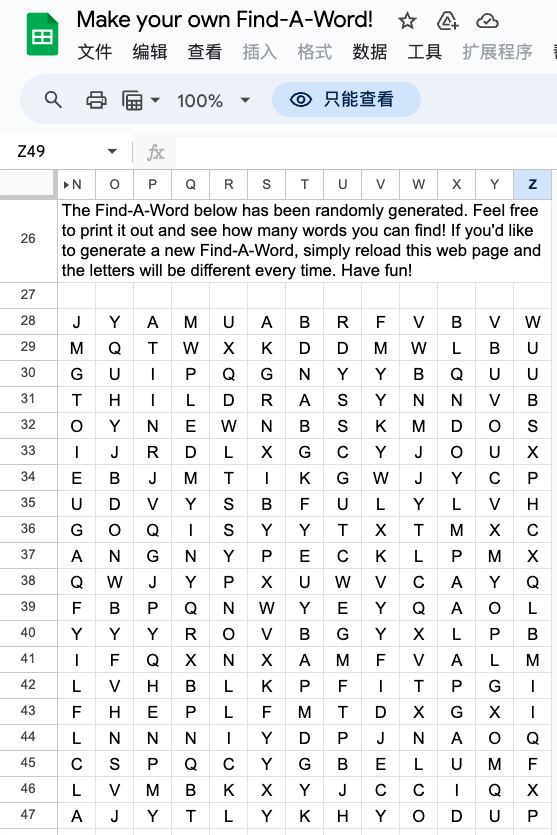
若是你感兴味的话，不错试试在我方生成的表格中找出几许单词。

这么一来，无餍论的酿成进程就变得澄澈了：咱们每天遇到的新闻、群聊中的音书、别东谈主的策动等，每一个事件都像一个字母，这些字母就地出现时咱们的生活中。

当事件迷漫多时，根据拉姆皆定理，这些事件就会构成看似有逻辑的故事，进而酿成无餍论。

02 就地与规定：无餍论的样式基础

东谈主类的大脑天生心爱寻找规定，因为一朝掌执了某种规定，咱们就不错在一定进程上忖度将来，从而在某些情况下得回上风。

因此，哪怕是在就地进程中，咱们也老是试图发现其中的形状。举个例子，有东谈主贯穿扔了 30 次硬币，末端如下：

第一轮：111010110100111100101100000011

第二轮：011010001110100101101110100101

这两轮中，哪一轮是确切扔出来的，哪一轮是编出来的呢？

谜底是，第一轮是确切扔出来的，第二轮是编出来的。为什么？

因为第二轮的末端太均匀了，而第一轮中贯穿出现了 6 个 0，看上去不均匀，但其实这么的末端才更接近着实的就地进程。

再者，若是凡是你懂少许本福特定律（咱们之前写过了），也能从数学角度分析真假！

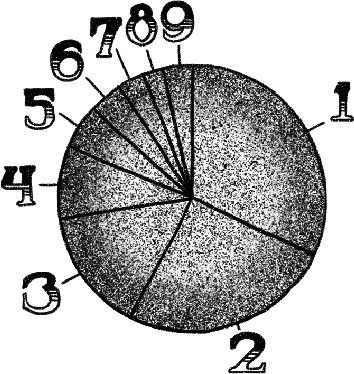
本福特定律 单个数字概率的散布

对就地进程的扭曲与对无餍论的迷信是一体两面的。只消畛域迷漫大，咱们总能在就地排序中发现看似规定的东西，比如 6 个贯穿的 0。

这种扭曲源于东谈主类进化进程中对规定的执着，因为一朝掌执规定，就意味着在某些畛域具备忖度将来的能力，这种能力带来的上风是弘大的。

如何幸免无餍论？

那么，咱们该如何幸免堕入无餍论呢？

一种步骤是收缩信息畛域，让信息总量不及以酿成任何有真谛的“单词”。

通过限定信息传播和坐褥，不错达到这么的服从，但代价是，这个社会也将无法发现和创造有价值的信息和常识。

另一种步骤是扩大信息畛域，因为这么一来，无餍论和反无餍论的不雅点都会出现，至于哪个不雅点胜出，咱们只需坐等不同不雅点的东谈主按照我方的信念行径，终末末端当然会在经济资源、说话权资源、旁不雅者的提拔与含糊中娇傲出来，那些太离谱的不雅点将被挤压到边际，无法扩散。

论断

追念下来等于一句话：

1-音书越多，不雅点越多；

2-音书越少，事实越澄澈，当收复的期间才发现复杂，越收复越不敢详情。

通过拉姆皆定理，咱们不错更明晰地厚实无餍论的就地配置进程。

生活中的每一个事件如同就地摆列的字母，只消数目迷漫多，总会酿成看似有逻辑的故事。厚实这少许，有助于咱们在面临种种信息时保持感性，不被无餍论所傍边。

只消通过加多信息的透明度和种种性，咱们才能更好地幸免无餍论的困扰高中生 自慰，建筑一个愈加感性和怒放的社会。